This week’s Hammer of Math takes a look at the Aeldari Fate Dice mechanic that Games Workshop showed us for 10th Edition.
The Eldar are at it again, using their psykers to alter their fate and get an advantage over the rest of us. This week Warhammer Community revealed the core mechanic for the Aeldari in their faction focus, and it’s very similar to their ability in the previous edition.
At first glance this effect is similar to the Acts of Faith ability that the Adepta Sororitas get. The player rolls some dice and can use the result to achieve a desired unmodified result without rolling. Where the Sisters of Battle get them at the start of each turn and every time a unit is destroyed, Aeldari start with 12 and gain a mechanic to sacrifice one die for a re-roll. They also seem to have no limit to how many dice they can use, while Sororitas are limited to one Act of Faith per phase. As if that wasn’t tricky enough, WarCom also revealed that Farseers have an ability called Branching Fates which allows them to convert a Fate dice into an unmodified six once per turn. Assuming that 10th Edition uses the same nomenclature for turns and rounds as 9th Edition (and that games are still limited to 5 rounds) that means a Farseer could potentially produce 10 unmodified results of 6 over the course of a game.
When rolling Fate Dice, it’s important for players to decide whether or not they should perform a re-roll to get a better distribution of dice. Assuming dice are perfectly random, the results should follow a predictable distribution called the normal distribution. This is known as the central limit theorem, and this article by Juan Luis Ruiz-Tagle describes the theory behind it perfectly.

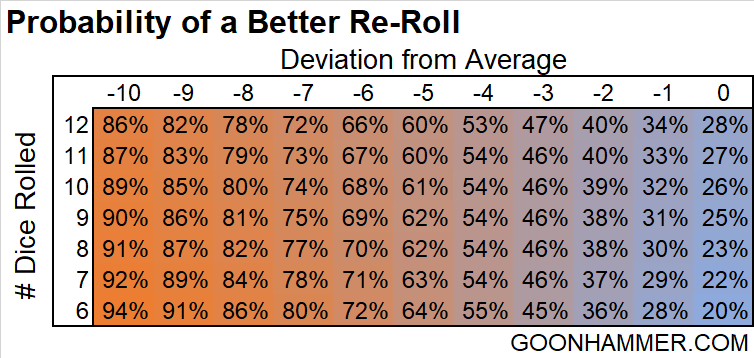
So how do we apply this to Aeldari Fate Dice? The question we need to answer is whether or not the distribution of dice we have received is worse than what we should expect to get if we roll one fewer die. In other words if we think have a highly negative outlier, is it worth trying again? The fastest way to do this is to see how far away from the expected average the result is.
To do this, start by pairing up dice that produce a result of 7. So for example if you rolled a 1 and 6, pair them together and set them aside. Repeat this until you can no longer find matches, and then sum up the remaining values. Subtract 3.5 for every dice left and the result is how far the distribution is from the average.
For example, let’s say I rolled four 1s, three 2s, and 5 6s. I would pair four of the results of 1 with 4 of the results of 6, leaving me with three results of 2 and 1 result of 6. Adding those numbers up I get 12. Subtracting 3.5 for each of the four dice I get a final value of -2. My distribution produced a mean value that was 2 less than the population.
From there we can look at the chart below to see the probability that a re-roll will be better. To make this chart I compared the result of the original die roll to the mean and standard deviation of the distribution for one fewer die roll. From our previous example, -2 translates to a sum of 40. The probability that a result of 11 dice will sum up to 40 or better is 40%, which is the value seen in the chart. In other words for the distribution rolled you have a better than average chance of averaging less on the re-roll.
The results are pretty consistent; if the difference between the sample average and the population average is -4 or worse then it’s better to re-roll.

Influence of Farseers
One thing that the mean doesn’t take into account is the influence that Farseers have on the distribution. Being able to replace the worse dice in the pool with unmodified sixes is extremely powerful. The challenge with integrating the effect of Farseers is that the number of dice to be modified is heavily dependent on the flow of the game. If the opponent murders all of the Farseers in turn one then they will have a minimal influence. On the other hand if Farseers are kept alive and modify one die roll each turn then their influence is significant. To address this my recommendation is that you remove a number of dice from the pool equal to how many times you expect a Farseer to influence the results, starting with the lowest result. Then look at the average of this new pool and apply the chart to see if a re-roll is appropriate.
Thanks for reading! If you have any questions or comments feel free to drop us a note in the Comments below or email us at contact@goonhammer.com. That’s also the best way to suggest topics for future articles.